The Great Regression — with Python: Fixed Effect Regressions (Part I)

In my last post, I discussed the experimental design for comparing the effect of an event on two groups (treatment and control groups). The example showed no significant effect, i.e., no difference between the groups, for the intervention discussed.

But is this true? The result could be correct and there is indeed no detectable difference (all good in this case 🙂). On the contrary, the true effect may be masked by so-called unobserved (or uncontrolled) heterogeneity (not so good 🙁). That’s where we left off.

Let’s revisit the topic and I’ll walk you through strategies for dealing with the problem of unobserved heterogeneity with another type of regression — Fixed Effects Regressions and Random Effects Regression.

Intuitive Description of the Problem

Unobserved heterogeneity occurs when there are underlying factors that affect the outcome of our model because there is some difference between our two groups that we do not account for. We do not include (or control for) this in the model.

This is often the case when working with panel data, that is, data collected over time for the same cross-section. There are two challenges that cause unobserved heterogeneity:

1. How do we know what to control?

Relationships between features can be complex and hidden in many real-world examples. If the relationship is hidden, we would not know that we need to control for it in the model, resulting in what is called Omitted Variable Bias (OVB), which obscures our results. This is most likely the reason for the null effect in the last post, since we didn’t include any controls.

2. What if we cannot measure what we want to control?

In many scenarios, data is sparse or only available at a higher level of aggregation. Thus, we may be aware of an important underlying relationship, but cannot account for it because of data issues.

This is where the Fixed Effects (FE) model and its close cousin the Random Effects (RE) model come in.

Formal Description of the Problem

Now that we have discussed the underlying problem intuitively, let’s formalize it. Suppose our regression model looks like this:

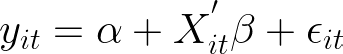
with the components of:

• y is the outcome (target) for individual i at time t (e.g., wage)
• α is the constant (intercept)
• X is a vector of observed regressors (features) and ß the associated coefficient (e.g., education)
• ε is the error term for individual i at time t

The problem of unobserved heterogeneity arises because the error term actually has two terms. This is why it is also called a composite error:

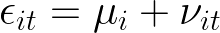
where:

• µ is the (individual) fixed effect for individual i, i.e., our unobserved heterogeneity. It includes everything that is specific to individual i but constant over time, such as a person’s place of birth, impacting the the included regressors (X).
• ν is the idiosyncratic error. This is the rest (all other variables) that is unobserved for individuals over time but unrelated to our regressors (X), i.e., this is the usual error (or uncertainty) being modeled.

Because of the presence of µ and its relationship to X, our model is incorrect unless we remove the effect of µ. Thus, the estimated effect is biased.

Both Fixed Effects (FE) and Random Effects (RE) models deal with unobserved heterogeneity (µ), but make different assumptions about the error term, as we will see.

The Fixed Effects (FE) Model

The FE model is a strategy to remove the unobserved heterogeneity from our specification. It assumes that the unobserved heterogeneity (µ) is uncorrelated with the error term.

The Fixed Effects strategy can be implemented in three ways:

1. Time-Demeaning

Time-demeaning is also called Within-Transformation because it considers one individual at a time (you can think of it as staying within an individual observation). To achieve demeaning, the individual mean (across all time periods) is subtracted from each observation of the individual. Formally, this means:

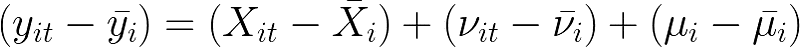
where µ drops from the model (i.e., is averaged out) because it is constant over time such that 

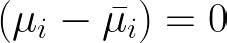
The resulting model can be easily estimated using the Ordinary Least Squares (OLS) algorithm, as shown in this post.

2. Least Squares Dummy Variable (LSDV) Model

With LSDV, the model is extended by introducing a series of dummy variables for each category (aka a binary variable that takes values of zero and one).

For example, we want to include the categorical variable ability (however it is measured) as unobserved heterogeneity related to education, which has three potential outcomes in our dataset: high, medium, and low. We would dummify the ability variable into three separate variables, each of which can only take the values 0 and 1 indicating the individual’s level of ability. However, estimating the model with dummy variables introduces the dummy variable trap. So be careful. The dummy variable trap means that one of the binary variables must be omitted to avoid multicollinearity problems. The remaining coefficients are interpreted in terms of the omitted category. For example, if the low ability variable is omitted, the interpretation of the coefficients of the remaining two ability variables is relative to the low ability variable (the reference group).

3. First Differencing

First differencing transforms the data by calculating the difference between point t and t-1. Formally, the idea is as follows:

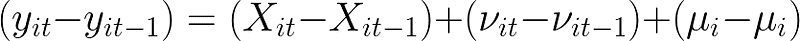
where

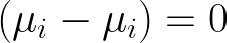
The unobserved heterogeneity falls out of the model because it is constant over time.

The Random Effects (RE) Model

The Random Effects model is similar to the Fixed Effects model, but assumes that the unobserved heterogeneity is uncorrelated with each explanatory variable in all time periods. This means that hidden characteristics have no relationship with the variables included in the model. This is a much stronger assumption than in the FE model.

For example, if we were to estimate the following model

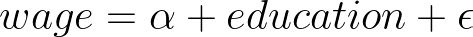
where we estimate the impact of education on wages. If ability is the unobserved heterogeneity (and thus hidden and included in the error term), then the RE model assumes that ability is uncorrelated with education. This assumption is unlikely to hold in many real-world settings, making it difficult to justify the use of an RE model.

Differences between Fixed Models and Random Models

The obvious question is how to decide between the two models. Let me give you a short list that might help.

The Fixed Effects (FE) model…

• is less efficient, i.e., it produces larger standard errors than the RE.
• cannot identify the effects of time-invariant variables because all FE strategies remove the constant terms. However, they are controlled for because they are included in the model, making FE a powerful tool for avoiding Omitted Variable Bias.
• assumes that the unobserved heterogeneity (µ) can be correlated with the explanatory variables, which is a weaker assumption than for RE models. For this reason, FE models are typically used more often than RE models because reality makes this assumption difficult to maintain.

The Random Effects (RE) model…

• is more efficient than FE, i.e. it produces lower standard errors (under the same specification).
• can estimate the effect of time-invariant variables. These variables are omitted in FE models because including dummies/using demeaning/using first differences removes the time-invariant variables and thus their effect cannot be recovered with FE.
• assumes that the unobserved heterogeneity is (µ) uncorrelated with each explanatory variable in all time periods. As discussed above, this is a strong assumption.

In addition, there is a formal test that can be helpful in choosing between the two models — the Hausman test.

The test checks whether µ (uncontrolled heterogeneity) is uncorrelated with the regressions. Formally, this means

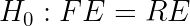
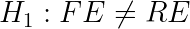
If H0 is rejected, use the FE model to avoid the Omitted Variable Bias. If H0 cannot be rejected, go with the RE model to get the higher efficiency.

In reality, however, the Hausman test almost always rejects the H0 hypothesis, indicating that the FE model should be used, as many researchers do. The question is how useful the Hausman test is and whether the uncorrelation assumption of RE models is too strong to hold in reality.

Extension: Two-way Fixed Effects model

So far, we have discussed how to deal with individual unobserved heterogeneity. Even more common in reality is a situation where not only a time-invariant but also an individual-invariant component forms the unobserved heterogeneity. For our regression setup, this means:

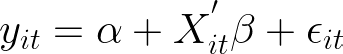
where the composite error now has an additional component.

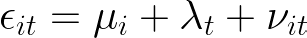
where:

• μ is the individual unobserverd heterogeneity (time-invariant) as before.
• λ is the time-unobserved heterogeneity (individual-invariant), which is the new part in the two-way FE model.
• ν is the idiosyncratic error as before.

The strategies for dealing with both types of unobserved heterogeneity carry over from the one-way scenario discussed earlier. For example, for demeaning, you would now demean by time and individual to get rid of μ and λ. I’ll walk you through it in the next post.

Summary

We had a look at an extremely powerful and widely used method in the social sciences to account for unobserved characteristics — the Fixed Effects/ Random Effects method. We have discussed:

• the problem at hand (intuitively and formally)
• strategies to deal with it — Fixed Effects (FE) and Random Effects (RE)— and their implementation strategies
• the difference between FE and RE models
• an extension to two-way FE models

In the second part of this post, I’ll walk you through the implementation strategies of the different methods in Python. So stay tuned.

Thank you for reading!

Check out my GitHub for other projects. You can also read the story on Medium. Feel free to reach out on LinkedIn.